This essay considers the problem of counting a large number of objects by a human. While counting large quantities of objects may not be an everyday necessity (unless you are a poker player), it is an intriguing thought experiment to explore how we can design approaches around human limitations. Logarithmic counting offer a lens through which we can examine our cognitive abilities and devise methods that cater to our strengths and weaknesses.

Main Text

Humans excel in recognizing specific patterns, those connected to our evolutionary past. For example, in the past we didn’t quite need to know precise counts of objects. It makes a difference if we have one or three predators chasing us, but the difference between ten and fifteen is clearly not as significant (the impact of different counts, in some sense, has a logarithmic shape). Our ability to quickly enumerate even small sets of objects is therefore quite limited. See, for example, the two following figures. Clearly, you need to struggle to count the number of elements in these lists.

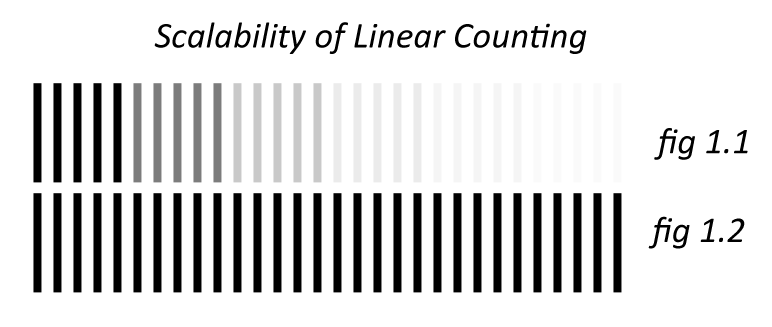
As numbers grow, enumeration becomes increasingly error-prone and tedious. To fix this issue relating to our capabilities, we can reframe the question by dividing objects into groups, creating a one-level hierarchy.

While helpful, this approach has its limits. Recursion becomes necessary to address the problem at various scales, allowing us to explore a counting method that adapts to human limitations.

Within the constraints of practical two-dimensional media, we can design multi-layered hierarchies.

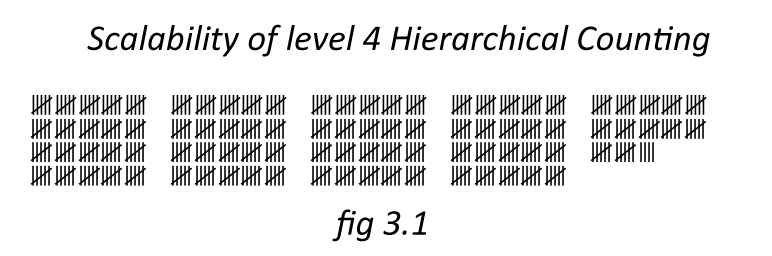
In the example above, a 5-5-4-5 hierarchy is depicted. Each row (level 2) contains 25 objects, each block (level-2) has 100 objects, and each row of blocks holds 500 objects (level-3). This spatial arrangement leads to recursion, with level-4 forming a block of blocks.

However, hierarchies come with trade-offs. Spatial efficiency is sacrificed in comparison to the initial linear arrangement.

Our choice of 4 or 5 objects per level is intentional. Humans can count 1-5 objects almost instantaneously, an $\mathcal O(1)$ operation. Beyond that, we resort to linear counting, an $\mathcal O(n)$ process. By implementing a logarithmic hierarchy, we create a counting system better suited to our cognitive strengths.

By utilizing 5 meta-items per level, a capacity of $5^n$ items can be achieved with $n$ levels, requiring roughly $n$ operations. This is the essence of logarithmic counting.

Conclusion

This thought experiment on logarithmic hierarchies provides an opportunity to reflect on human cognition and consider how we can adapt methods to accommodate our limitations. While not directly applicable to everyday life, it offers insights into potential ways of handling complex tasks. The exploration of human capabilities through such thought experiments can pave the way for innovative solutions and inspire new approaches to task execution.