The Enlightened Gambler: A Sobering Simulation of the Doubling Method
Contents
In conversations about gambling, I frequently encounter a dangerous cocktail of misinformation and misunderstanding. The average person, quite understandably, grapples with comprehending how probabilities can guarantee long-term losses. This challenge is further exacerbated by fallacies and complicated games that intentionally obscure the underlying truth: the house always wins.
To illustrate this point, I’ve chosen to simulate the gambling process and present the average outcomes rather than diving into a potentially confusing sea of probabilities.
The Doubling Method: Roulette’s Deceptive Allure
The doubling method, or Martingale system, is an alluring strategy that promises modest winnings at a high probability. However, it comes with the catch of potentially colossal losses at a low probability. This house advantage ensures that, in the long run, you’re fated to lose your money.
Note: It's worth noting that while many of us are staunchly opposed to casinos, we often unknowingly indulge in gambling through other processes. For instance, some people believe they're profiting from trading, only to suddenly realize they've been playing a game with low winnings at high probability, massive losses at low probability, and an overall negative expected value. This concept is explored in greater depth in the book "Fooled by Randomness" by Nassim Nicholas Taleb.
To visualize this reality, I created a Python program to simulate the strategy, starting with 2000 USD in your pocket and a reset-bet of 2 USD. In each session, our simple goal is to earn varying amounts of money before exiting the casino to bask in the glory of our easily-earned gains. Note that we’re making the significant assumption of no betting limit.
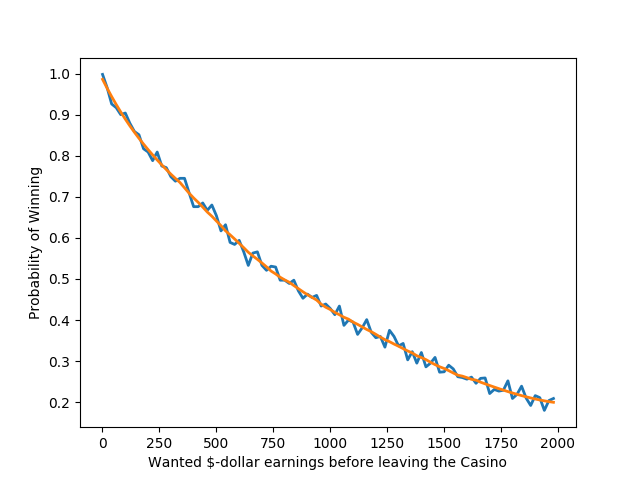
A Meta-Casino-Game Generator
The above graph is intriguing as it empowers you to generate a meta-casino-game: an unfavorable virtual game with the depicted winning probabilities, corresponding to your virtual bets. This peculiar idea warrants further exploration in a future post.
Suppose you’re in dire need of 250 USD and willing to risk 2000 USD. The graph indicates a ~75% chance of attaining the desired sum. It might seem like an acceptable gamble, but don’t let it seduce you!
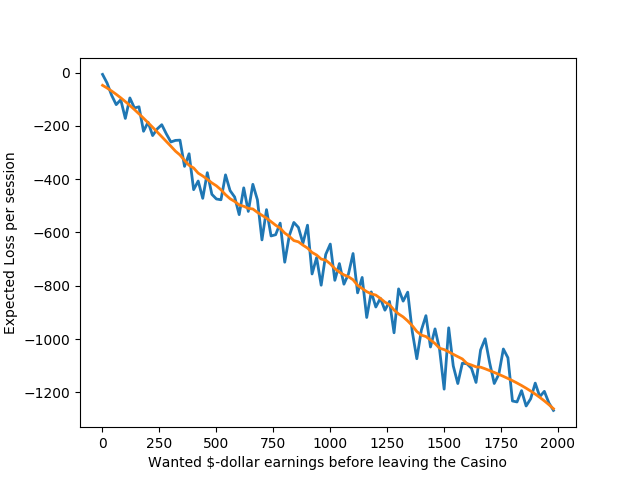
The second graph reveals why you should never rely on this method: the expected outcome is losing money.
To estimate your actual “winnings,” multiply the vertical-axis value by the number of times you plan to apply this strategy. For example, attempting to earn 500 USD a hundred times will likely cost you around 100x400 USD.