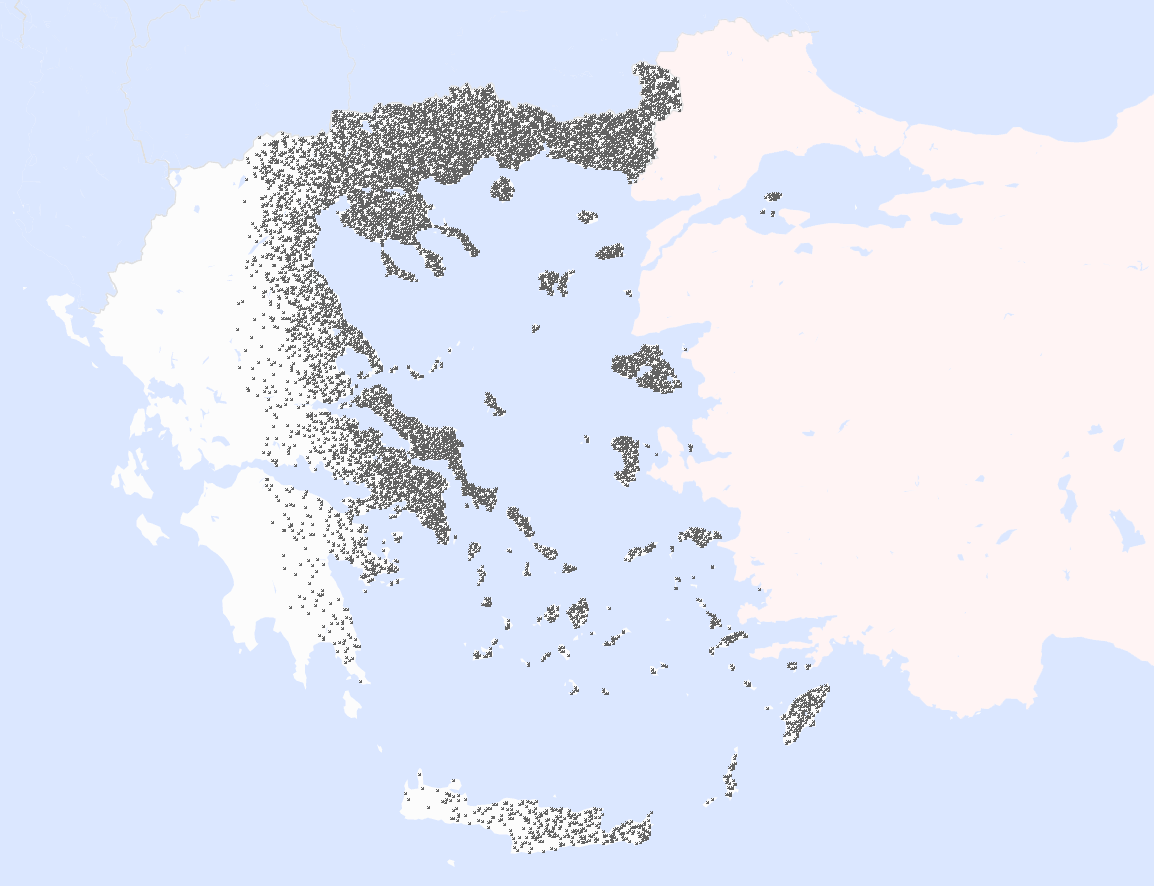
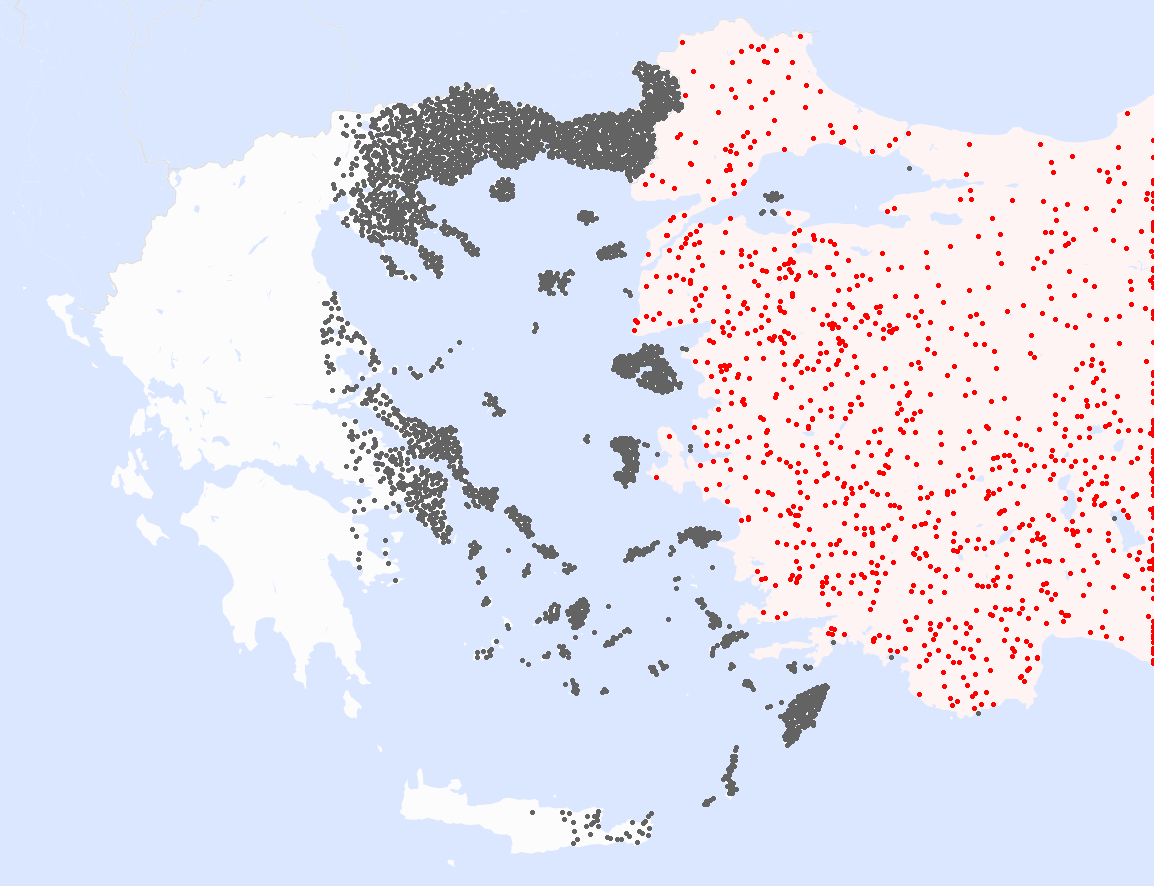
It was announced in Greek media that Turkey achieved a new maximum range with modern missiles in its disposal. I was instantly curious: what targets in Greece can be hit by Turkey now?
This experiment is created for fun. The author is optimistic about the relations of the two countries.
scroll down for the results to see the resulting images
Problem Setting
Hit Area
Let $\mathcal{T}$ be the set of points that are in Turkey. \(\mathcal{G}\) the set of points in Greece. The range of the missile \(R\), then we are looking for:
$$\mathcal {Hit} = \{ x \in \mathcal G\ |\ y \in \mathcal{T}: ||x-y|| \leq R \}$$
Accessibility of Targets
It might be of interest to measure how easily a target can be hit, that is, how many points in Turkey’s territory have access to the target.
This can be computed by the area of the points that can reach the target:
$$\mathcal{Acc}(x) =area\ \{ y\ |\ y \in \mathcal{T}, ||x-y|| \leq R \} $$
Implementation
There are many ways to implement this. Sophisticated solutions would yield a precise image of the targets that can be hit (computational geometry might be of use here).
In this project we are looking for simple Monte Carlo solutions. Consider this very direct approach: take random points in Turkey’s territory using rejection. For a random point in Turkey \(p_t\in \mathcal T\), take random points \( \{p_i\} \) within the range of the missile: \( p_i \in \{ p\ |\ ||p-p_t|| \leq R\}\). Keep the points that fall in Greek land \( \{p_i\} \cap \mathcal G \).
Limitations of approach. This approach would not be as efficient for extremely small areas.
Other Monte Carlo Methods. We don’t use domain knowledge in this approach. Countries tend to be concentrated in certain areas as opposed to be sets of arbitrary points. Smarter sampling would take advantage of structure like this to uncover better sample efficiency. The interested reader is referred to MCMC methods.
Final Image
Two different pictures of two different ranges are shown. The second image depicts the random points from which we started in Turkey.
The side effect of this implementation is that density also illustrates the accessibility of an area.