Concept

The concept is the following: Drop $N$ mice randomly in a rectangular area. Each mouse targets exactly one other mouse forming a circle of targets.

$$M_1 \rightarrow M_2 \rightarrow … \rightarrow M_N \rightarrow M_1$$

All mice have equal velocity. The simulation follows. After clicking on the simulation, press (i) to increase the number of mice, and press (d) to decrease it.

Simulation

Emerging Behaviors

• Each mouse \(M_i\) is confined in the rectangular area. This is due to the fact that every mouse targets a point within the rectangular area at any point.

• Each mouse gets very close to its target mouse. Since the rectangular area is limited, a mouse has to change direction at some point. During this change, the pursuing mouse reduces the distance from its target (since they have equal magnitude of velocity). This is true until a lower-bound distance is reached, after which “the reaction time” (alternatively, due to the discreteness of the simulation) of the mouse is slow and the distance can not be further reduced.

• The mice reach a steady state behavior, circulating on a path.

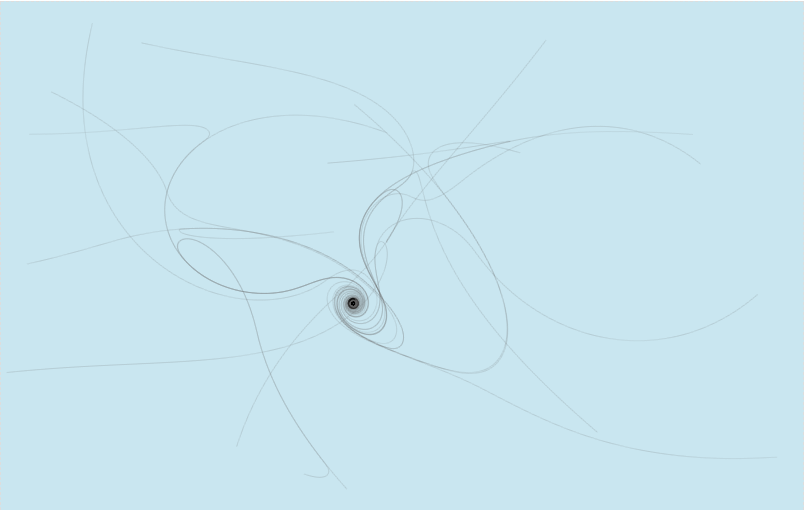
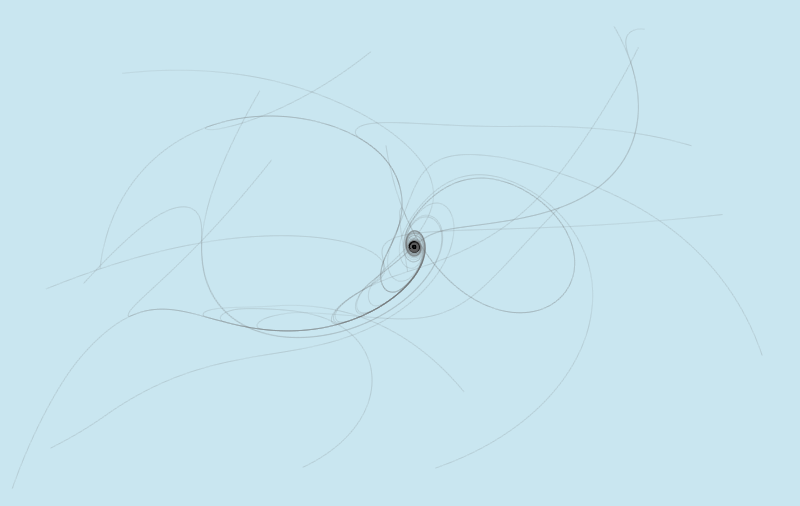
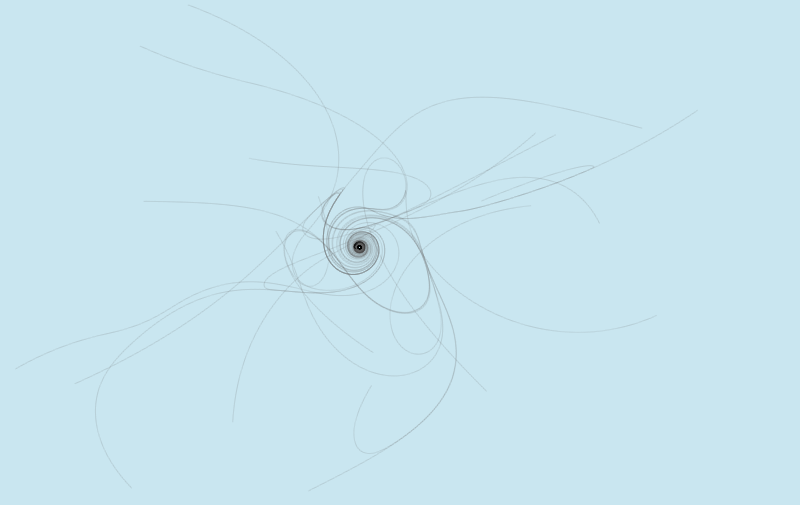
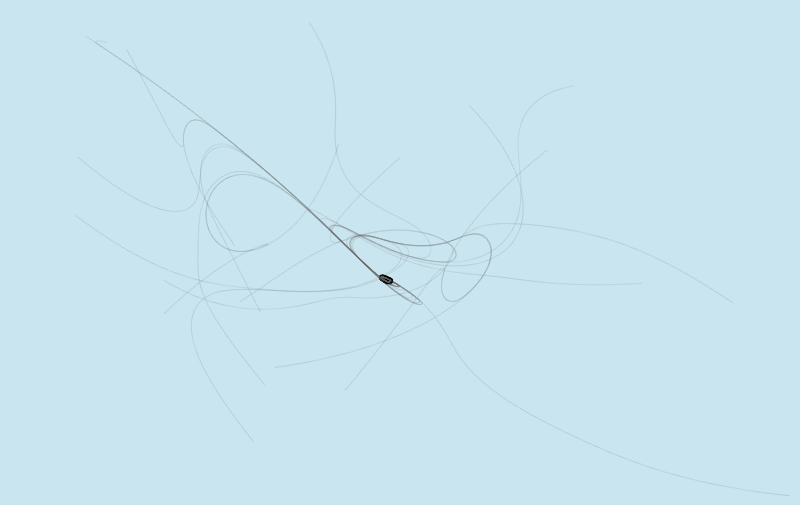
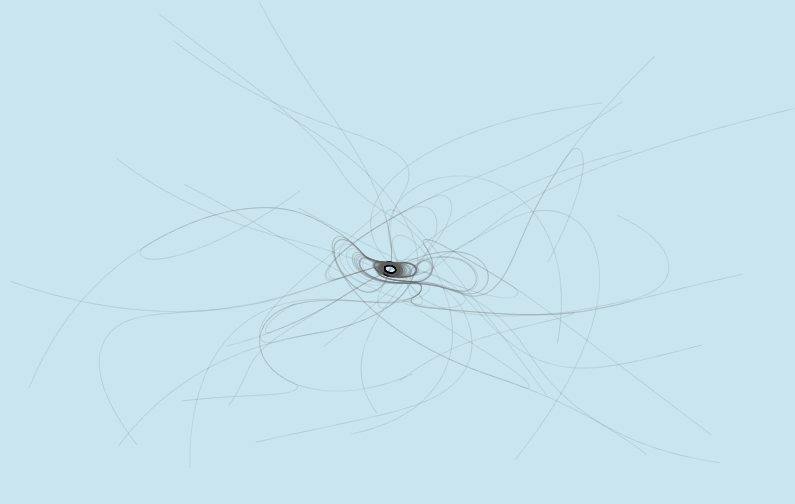
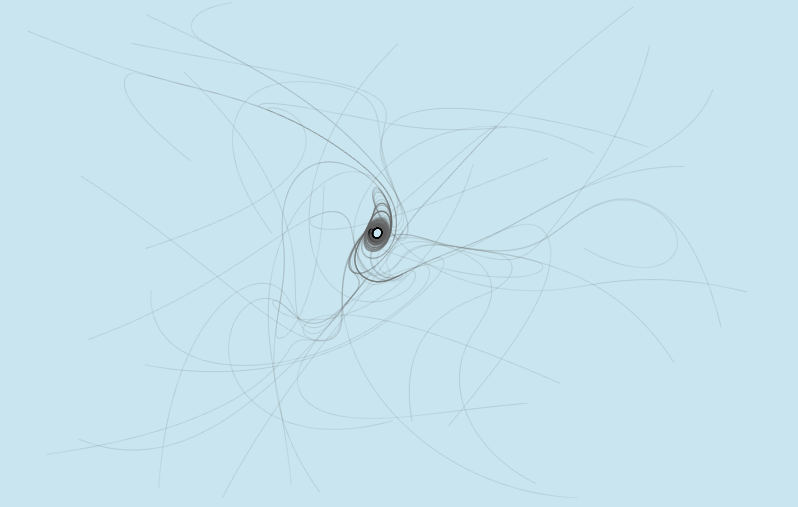
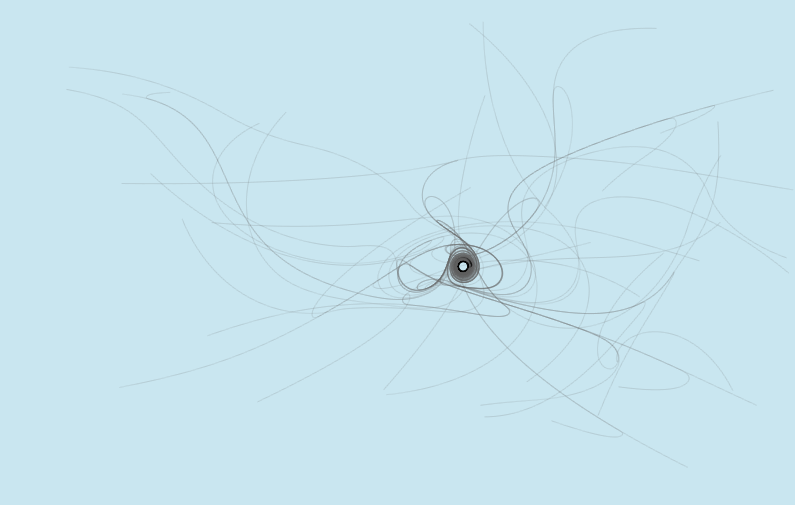
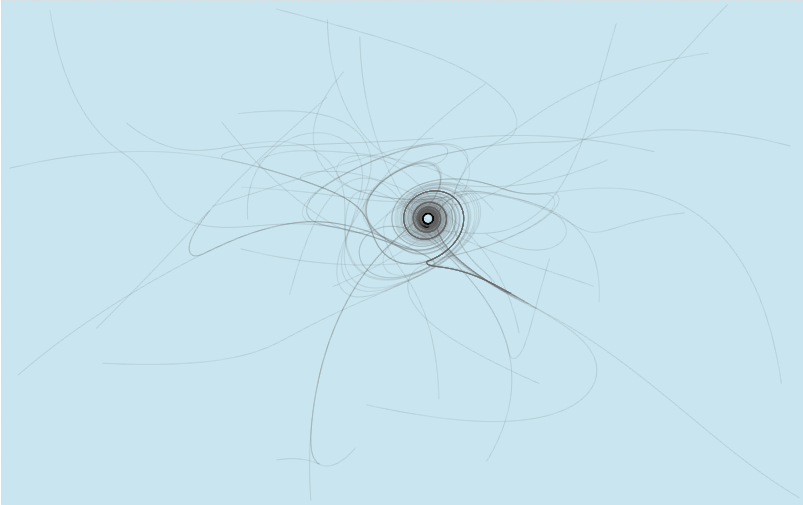
• Usually a loop of mice emerges. The more the mice deployed, the bigger the length of the curve.

Example Instances

The results below depict various realizations for different number of mice. Use the simulation above to get your own art!